Polar Curves

by Dermot Tynan in Microtransat

---

Posted on Thursday, March 07, 2013 at 08:00

---

Even before a boat is built, the designers can predict how fast it will go at various sail angles. Using this information, they can make modifications to the hull to suit the type of sailing. For example, if an around-the-world race looks like it will see a lot of downwind sailing, it's possible to optimise the downwind performance, and run test simulations with the boat, before ever committing to fibreglass.

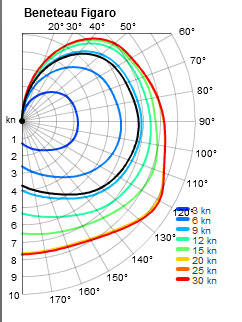
The standard mechanism for displaying this information is a polar curve. Because the boat should sail at the same speed on either tack, only one side is shown. Essentially, a polar curve allows the designer (and the boat owner) to predict the hull speed for a particular true wind angle and strength. In the example above (courtesy of SailOnline.org), you'll notice that the boats fastest speed is at a true wind angle of about 120 degrees. In the case of a 30 knot breeze (the red line), the boat should get over nine knots through the water. At TWA's of twenty degrees and less, the boat will stop, regardless of the wind speed.

As I mentioned in a previous posting, you can use this information to calculate the VMG of the boat. To remind you, the VMG is the "velocity made good" or the velocity not in terms of how fast we're going over the water, but how fast we're getting to the mark. If the speed over the water is V, and the angle between our heading and the bearing for the mark is alpha, then our VMG is Vcos(alpha). There are elements of angular velocity at work here, but we'll choose to ignore them, for now.

We can quickly see that an alpha angle of 90 degrees won't work. If the mark is directly off the beam (side of the boat) then no matter how fast we go, we'll never get to the mark. In point of fact, we'll move away from it because we're in a straight line, not a circular path. cos(90) is 0, so this just proves that we'll have a VMG of 0 regardless of our speed. Conversely, an alpha of 0 would be ideal, because every ounce of speed is towards the mark. That's fine for downwind, but as you can see from the polar, if the mark is directly upwind of us, sailing to that course would give us a boat speed of 0 knots. So, we have to find the compromise. When you're racing, you'll generally pull the boat up as close to the wind as you can. For a racing boat like the manic Figaro above, this is around 30 degrees off the wind. We'll make a hefty 5 knots of hull speed in strong winds, according to the polar. Our VMG would be 4.33 knots. This makes sense. But if we were to fall off the breeze a little bit, and drop down to 50 degrees off the wind (and off the mark) then we'd speed up to 7 knots. Impressive! But we're moving away from the mark much more dramatically. The thing is, our VMG is 4.499 knots. That's a significant difference. In this case, the best course for the mark isn't to go as close to the wind as possible, but to ease off and sail to the polar at 50 degrees.

Those are just two angles I chose for convenience. There is probably a better solution in there, possibly at 45 degrees, but I'll leave that as an exercise to the reader.

When you're out on the water, particularly in a dinghy, with spray in your face, someone out on the trapeze, other boats in the vicinity, and all of the adrenaline associated with getting to the next mark, it's hard to think in terms of polars and VMG. On bigger boats, they'll often tape a sheet of ideal VMG curves onto the cockpit so that the trimmer and helmsman can see the angles, rather than compute them.

Things are a little different for Beoga Beag. She has an onboard computer that's just dying to compute ideal VMGs. With Otto taking care of steering the boat to the TWA, Mother can devote all her time to deciding what the best TWA should be. Often, it makes for an interesting result! Early simulations showed a TWA of 53 degrees on an upwind leg. Also, due to the problem around tacking I mentioned previously, the boat tacked back and forth as every new computation favoured the opposite tack, naturally enough. I will have to add modeling to show the detrimental effects of a tack - that won't be trivial as it's an up-front cost, not an amortized cost.

In a later posting, I'll upload a screen capture of the simulated upwind leg. It's not pretty.

The other aspect of this which hasn't been considered so far, is that polar curves are ideal. They assume the boat hasn't heeled over, and that the water is flat. No such luck in the microtransat, unfortunately. Wave heights will be on the order of 4 metres, and wind speeds could average 25 knots or higher. Sailing just to the polar might be a good idea in lab conditions, or in simulations, but out there, it's a different story altogether...

---